Ptolemy’s work consists of a list of ca. 8000 place names in the Roman Empire of the 2nd c. AD (Stückelberger & Graßhoff, 2006). Each place is located with latitude and longitude aiming at enabling a reconstruction of the complete map of the world he was living in, but it is believed that he probably never published a drawing of such a map.
His latitudes are related to the equator, like we do today, and the value of one minute of latitude is 1852 m (or one nautical mile, by definition).
The value of one minute of longitude depends on the latitude: it is around one nautical mile at the equator and nil at the poles. Elsewhere its value is :
- 0.74 nautical mile in the south of France, or 1375 m at 42° of north latitude,
- 0.81 nautical mile near Rhodes, or 1500 m at 36° of north latitude,
- 0.85 nautical mile near Alexandria, or 1570 m at 32° of north latitude (NB: one degree of longitude in Alexandria is ca. 600 Egyptian stadia of 157.5 m),
- 0.97 nautical mile near Massawa and Dakar, or 1790 m at 15° of north latitude.
His reference point for longitudes is located at the Fortunate islands, somewhere west of Greenwich which is today’s reference. However, a shift increasing towards the east is observed: shift of 20-22° in France, around 25-30° in Greece and 35-40° in the Red Sea.
It appears that he also underestimated the value of one degree of longitude.
This subject has been discussed for nearly two millennia (!) … Without entering into this discussion, it appears quite clearly that Ptolemy’s ‘errors’ might be corrected by a combination of a shift and a reduction factor.
We have therefore carried out an analysis (called ‘linear regression’) on a sample of 42 well known coastal sites by comparing Ptolemy’s latitude-longitudes with the present values.
The result is so clear that it is worth showing here:
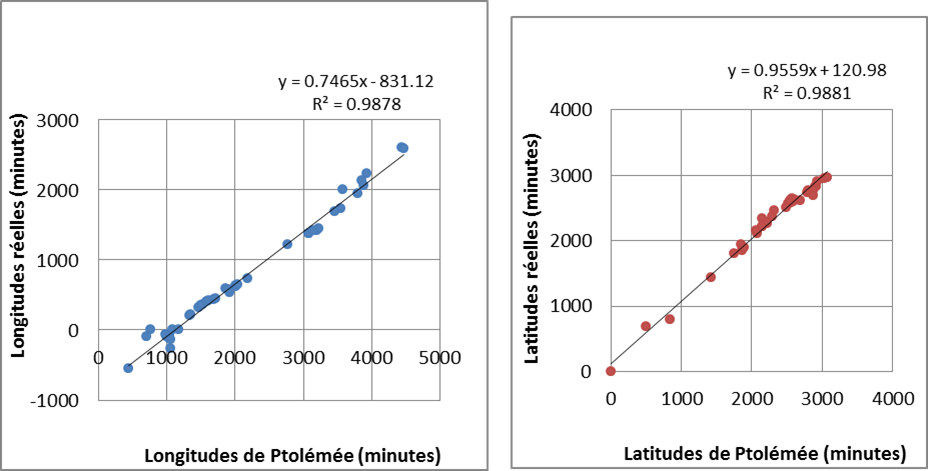
Ptolemy’s longitudes (left figure) and his latitudes (right figure) are set out horizontally; the real latitudes and longitudes are set out vertically. It can be seen first that the points are quite well aligned on straight lines (correlation coefficient R is 0.994) which shows that the mathematical formulation (“y = ax + b”) is correct.
The straight line for latitudes shows that Ptolemy’s values are, globally, equal to the real values (factor 0.9559 close to 1, and shift of 120.98 minutes; that is still 2°).
The straight line for longitudes shows a larger correction than for the latitudes:
Longitude (minutes) = 0.7465 x Long. Ptolemy (minutes) – 831.12 minutes, which can be rounded to:
Longitude (degrees) = 0.75 x Long. Ptolemy – 14°
In other words, Ptolemy’s reference point is at 14° west of ours (Greenwich), which leads to the Canary Islands which are between 13°30’ and 18°, but not to the Cape Verde Islands which are between 22°30’ and 25°30’.
Apart from this correction of 14° for the reference point, Ptolemy’s longitudes are still too large and a fraction of only ¾ (factor 0.75) must be taken.
These figures would probably be confirmed with a larger sample of places than the 42 taken here.
A possible explanation is that Ptolemy chose to assimilate one degree of latitude (or longitude at the equator) with 500 Egyptian stadia as wrongly suggested by Marinus of Tyr, leading to a circumference of the earth of 180 000 Egyptian stadia; instead of nearly 700 Egyptian stadia as correctly suggested by Eratosthenes, deduced from a circumference of 250 000 Egyptian stadia as calculated by him from his measurements at Alexandria and Syene (Strabo, Geogr. 2.2 and Ptolemy, Geogr. 1, 7). The latter yields a circumference of 39 375 km, if Egyptian stadia of 157.5 m are used, and this is very close to today’s accepted equatorial value of 40 075 km.
It is thus noted that, at Alexandria, one degree of longitude measures ca. 600 Egyptian stadia, and one degree of latitude is ca. 700 Egyptian stadia.
When using Ptolemy’s data, we must realise that the accuracy of his latitude-longitudes is not very high. Basically, and as shown above, latitudes are more accurate than longitudes, as they can be checked with the Sun’s positions, e.g., the duration of the longest day of the year, while longitudes must be deduced from distances reported by travellers (without chronometers).
It was shown above that Ptolemy’s latitudes can easily shift by one or two degrees (around one hundred minutes in the figure above). It is noted also that all of Ptolemy’s figures for degrees of latitude and longitude are given with a smallest approximation of 1/12° or 5 minutes, in the oldest available manuscript of 1460-1477. In the 1562 manuscript, the translator provides figures in degrees and minutes and the latter are all multiples of 5 (NB: some “6”s are found on the lists and may probably be considered as copyist confusions between a “5” and a “6”. I therefore took the liberty of replacing “6” by “5” in the 1562 manuscript). This indicates an estimated precision to + or – 2.5 minutes (around + or – 2 nautical miles). Ptolemy was therefore very optimistic on his precision!
Ptolemy’s work allows us to position ancient ports based mainly on their latitude.
It may be of interest to compare the longitudes of some places,
but only within a short distance.
Some recent publications on this topic:
References
- ARNAUD, P., 1990, “La cartographie à Rome”, Thèse d’Etudes Latines pour le Doctorat d’Etat réalisée sous la direction de monsieur le professeur Pierre Grimal, Université de Paris IV.
- ARNAUD, P., 2014, “Mapping the edges of the Earth: Approaches and cartographical problems”, Colloquia Antiqua, 12, ed. A. Podossinov.
- ARNAUD, P., et al., 2022, “Les alignements de points dans la construction des mers chez Ptolémée”, Sine fine, Studies in honour of Klaus Geus, edt. Soren Lund Sorensen, Franz Steiner Verlag, (p 55-71).
- BROUSSALIAN, E., 2019, “Ptolémée et Macoraba”,
- BUCCIANTINI, V., 2012, “The limits of knowledge : explorations of and information from the Horn of Africa to the East African coast in the Graeco-Roman tradition”, Topoi, Suppl. 11, 2012.
- DE GRAAUW, A., 2023, “Décrire le monde – La carte à la conquête du territoire”, published online on Herodote.net, May, 2023.
- FORSTNER, G., 2004, “Längenfehler und Ausgangsmeridiane in altenLandkarten und Positionstabellen”, Dissertation, Universität der Bundeswehr München.
- ISAKSEN, L., 2011, “Lines, Damned Lines and Statistics: Unearthing Structure in Ptolemy’s Geographia”, 6th International Workshop on Digital Approaches in Cartographic Heritage, The Hague, 7-8 April 2011.
- MARX, C., 2016, “The western coast of Africa in Ptolemy’s Geography and the location of his prime meridian”, Hist. Geo Space Sci., 7, 27–52, 2016.
- RUSSO, L., 2013, “Ptolemy’s longitudes and Eratosthenes’ measurement of the earth’s circumference”, Mathematics and Mechanics of complex systems, Vol. 1, No. 1.
- SHCHEGLOV, D., 2004, “Ptolemy’s system of seven climata and Eratosthenes’ Geography”, Geographia Antiqua 13 (2004), 21–37.
- SHCHEGLOV, D., 2020, “The configuration of the Pontus Euxinus
in Ptolemy’s Geography”, Hist. Geo Space Sci., 11, 31–51, 2020. - A. STÜCKELBERGER, A. & G. GRAßHOFF, G. (editors), 2006, “Klaudios Ptolemaios Handbuch der Geographie”, Basel.
- TUPIKOVA, I. & GEUS, K., 2013, “The Circumference of the Earth and Ptolemy’s World Map”, Max Planck Institute for the History of Science, Berlin / TU Dresden & FU Berlin.
and the complete initial texts available online:
- Ptolemaeus, Geography, Books II to VI, translation by Brady Kiesling, 2019, (in English).
- Claudii Ptolomei Cosmographie: Codex Valentinus, translation by Jacobus Angelus, Italy, 1460-1477, (in Latin).
- Geographia Cl. Ptolemaei Alexandrini : olim a Bilibaldo Pirckheimherio traslata, at nunc multis codocibus graecis colata, pluribusque in locis ad pristinam veritatem redacta a Josepho Moletio mathematico, 1562, (in Latin).