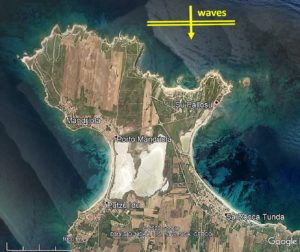
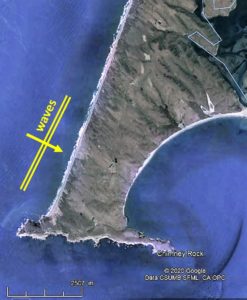
Our aim in this section is to describe some parameters defining the existence and the size of tombolos and salients. Much research on this subject has been done in the past 50 years because of its interest for coastal protection works like detached breakwaters, which are man-made structures placed parallel to the existing initial shoreline (see some references hereafter).
Islands connected to the mainland by an isthmus have been inhabited by people since prehistoric times and around 65% of those found on the Mediterranean coasts are ancient settlements.
Definitions
Strictly speaking, a tombolo is a sand spit connecting the mainland at a right angle to an offshore island or obstacle. A sand spit is often generated from the mainland to each side of the island. In the lee of a small island, both sand spits, or tombolos, will join as a single sandy isthmus, possibly leaving a triangular marsh area near the initial coastline. A large island may generate two separate tombolos and a large marsh area.
Note that some people call “tombolo” the whole mushroom-like feature including the sandy isthmus and the island, but geographers do not.
A rocky cape is obviously not a tombolo, even with a beach, as it does not have a sandy isthmus.
The Cap Serrat isthmus is small with a 160 m island, and the Mandriola isthmus with a 3600 m island, over 20-times larger, but the general geomorphological shapes are similar.
.
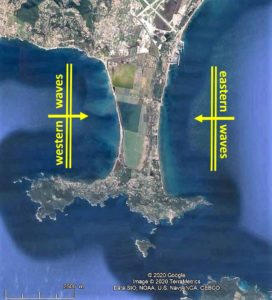
Coastal sands are moved along shores by waves with an oblique incidence. Wave crests nearing the coast are often more or less parallel to the initial shoreline (say with an angle smaller than 10°), and wave diffraction generates the typical symmetrical shape of the tombolos shown in the pictures above where waves come in from the top of the pictures. We might we call this “tombologenic wave-diffraction”.
Note that sand on each side of the isthmus usually has different origins, e.g., a river outlet on each side, and different wave directions move sand on each side towards the isthmus.
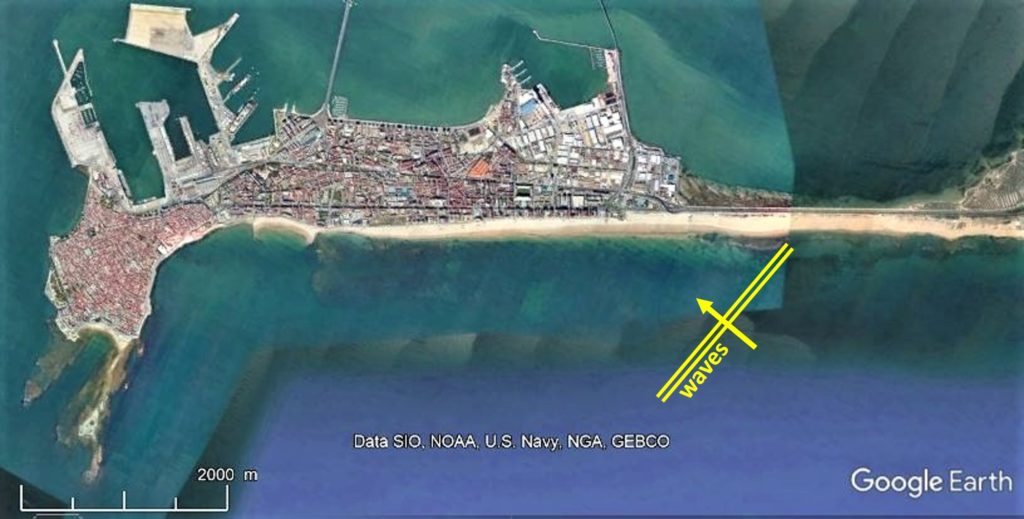
The famous Orbetello (Italy) and Giens (France) tombolo beaches are considered as independent beaches on each side of the island.
In the case of Giens, the eastern beach is fed by sand from the Gapeau river which is moved during eastern wave-episodes. On the western beach, sand is moved by western waves due to the Mistral wind but is barely fed by any coastal sediment and is therefore much thinner and retreating eastwards. The case of Orbetello has been excellently dealt with by Brocard et al. (2024).
If wave crests approach the island laterally, the isthmus has an asymmetrical shape with limited diffraction on the remote side, and such an isthmus is better thought of as a headland (e.g. Point Reyes, north of San Francisco, USA). We will not consider such cases in our study.
Similarly, in case wave crests approach the beach at an angle of 45° or more, a sand spit is generated. A true sand spit has a free end, usually turning around like a hook. However, in a few cases, such a sand spit may encounter an island (Cadiz in Spain, Chesil Beach in UK). As no wave diffraction is involved in that process, we will not consider such cases in our study.
Last, but not least, a bell-shaped salient occurs when the offshore island is smaller, or further away from the initial coastline, than in the case of an isthmus. Tyre (Lebanon) was a salient before the arrival of Alexander-the-Great in 332 BC. It became a tombolo after he built a causeway that became an isthmus.
In the case of oblique wave crests, the salient will be asymmetrical with its apex pointing away from the incoming waves.
It must be noted also that some alluvial fans (fluvial sediment deposit at the river outlet) may have the aspect of a salient, but they usually have no offshore island and no wave diffraction.
.
In our study hereafter, we shall concentrate on isthmuses and salients perpendicular to the coast and generated by wave diffraction. They can only exist if:
- the initial coastline is a sandy beach (or shingle),
- an island (or obstacle) yields an area sheltered from waves and generating wave diffraction,
- wave crests approach the initial coastline with an angle smaller than say 10°,
- no currents flow between the island and the initial coastline.
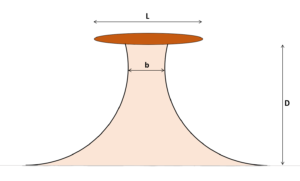
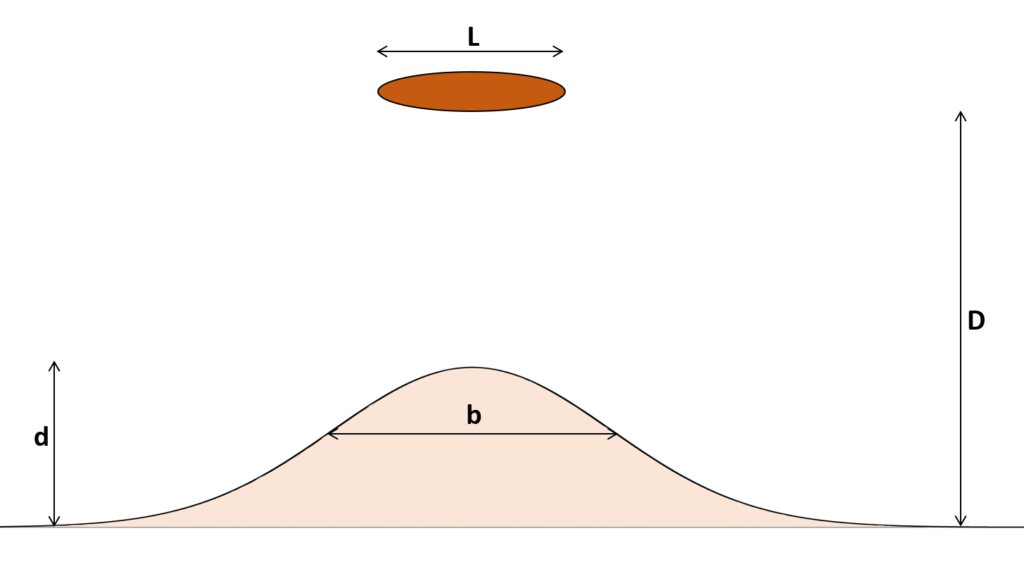
L is the length of the island and D is the distance from the initial shoreline. For isthmuses, we define b as the smallest width of the isthmus, and for salients, b is the width at the inflexion point, and d is the distance from the tip of the salient to the initial shoreline.
An isthmus is thus geometrically defined by L/D which is a constant in time, as long as the sea level is constant.
Formation
When offshore wave-crests approach the coast with a small angle (usually less than 10°, but in any case, less than 45°), they are subjected to refraction which tends to align the wave crest parallel to the coastline. If wave crests encounter an obstacle like a small island, they are subjected to diffraction which tends to turn the waves around the island.
When breaking on a sloping coastline, waves release their energy in turbulence and in longshore currents which may transport sediment (usually fine sand with a median diameter D50 of 0.2 mm to one or more millimetres). Shoreline forms are thus created by wave refraction and diffraction and longshore sand transport. The combination of these physical phenomena is complex but now well modelled in some physical scale models and in numerical so-called “one-line models” reproducing the shoreline.

The diffraction pattern is clearly shown on the picture above where breaking wave crests are always at a small angle with the shoreline. This implies that some longshore sand transport is ongoing from right to left, towards the isthmus. If you would walk from right to left on the beach shown on this picture, you would first see waves refracting during their approach to the shore (bottom right of the picture), then you would enter the curved shoreline where wave refraction and diffraction are combined (the shoreline shape is close to that of a logarithmic spiral). Finally, you would arrive in the lee of the detached breakwater and enjoy maximum shelter from offshore waves. It has been shown that a current system exists which forms a circulation cell turning in clockwise direction in the particular case shown on the picture above (Mory & Hamm, 1997).
Mediterranean isthmuses
Using Google Earth, we searched the 45 000 km of the Mediterranean Sea coasts to detect salients and isthmuses with two tombolos, and over 120 sites were listed. This list includes around 75 natural isthmuses and around 20 natural salients generated by offshore islands, islets or reefs. In addition, a few sites with man-made single or multiple detached breakwaters were listed.
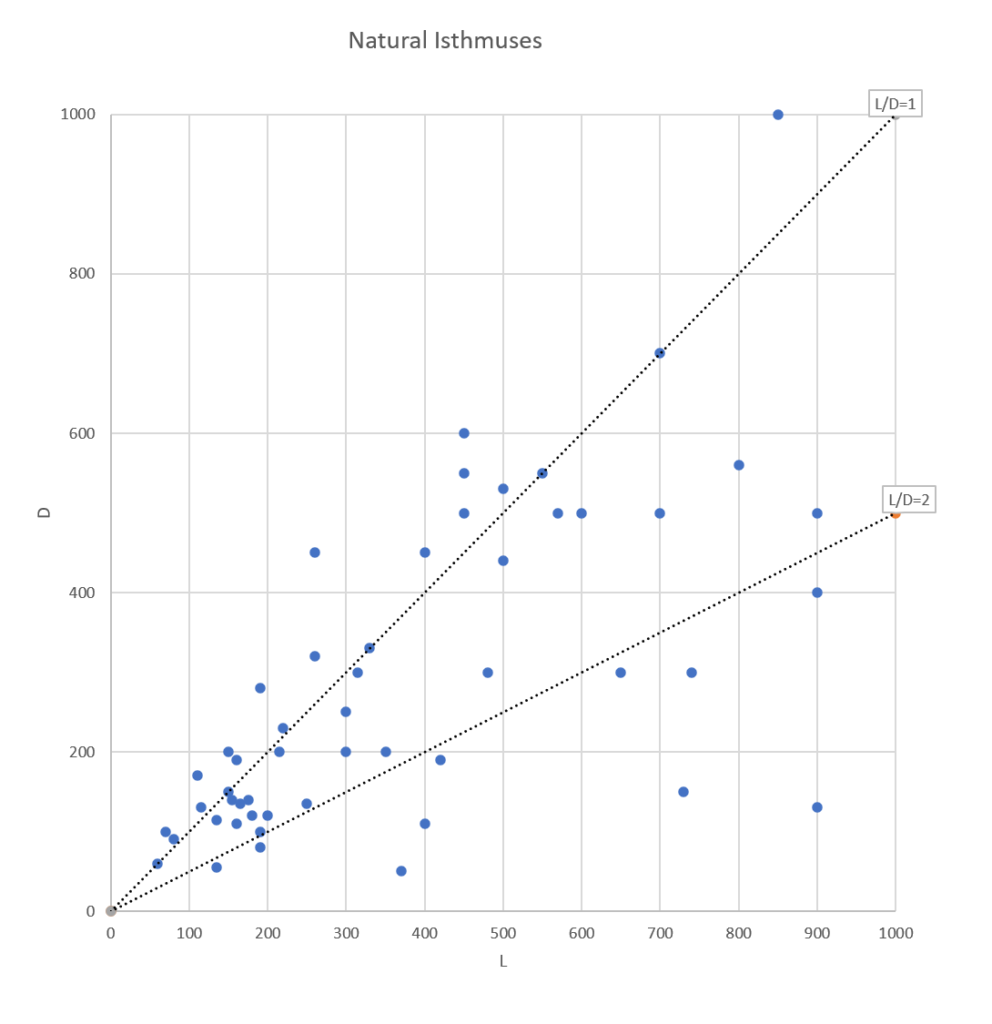
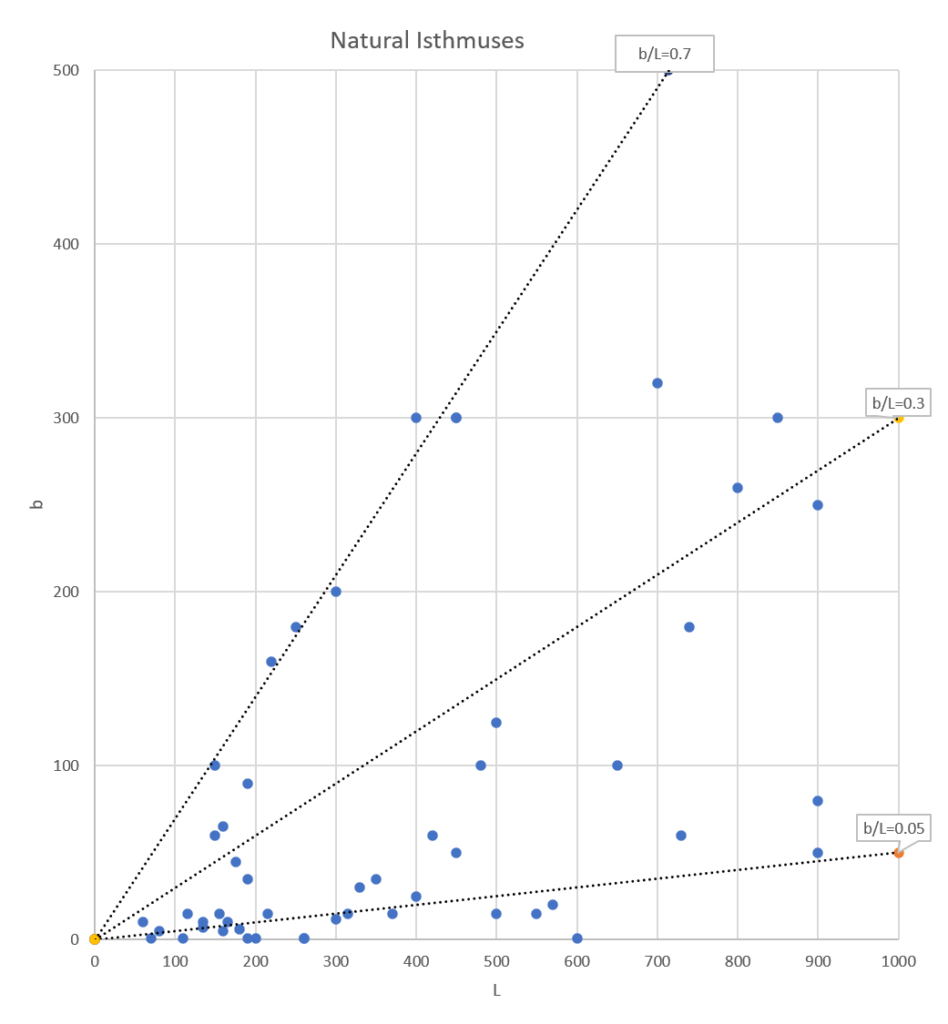
Let’s first have a look at the relationships between L and D, and b and D for natural tombolos:
Both figures show much scatter.
For D versus L, it may be seen that, very schematically, L/D = 1 to 2, with many exceptions.
For b versus L, it may be seen that b/L = 0.05 to 0.7 with much scatter. A kind of average at b/L = 0.3 corresponds very well to results given by Rosen (1982, fig. 8) who gives: a = 0.33 L, with a = (L-b)/2.
Let’s now have a look at a relationship between the dimensionless parameters L/D and b/L:
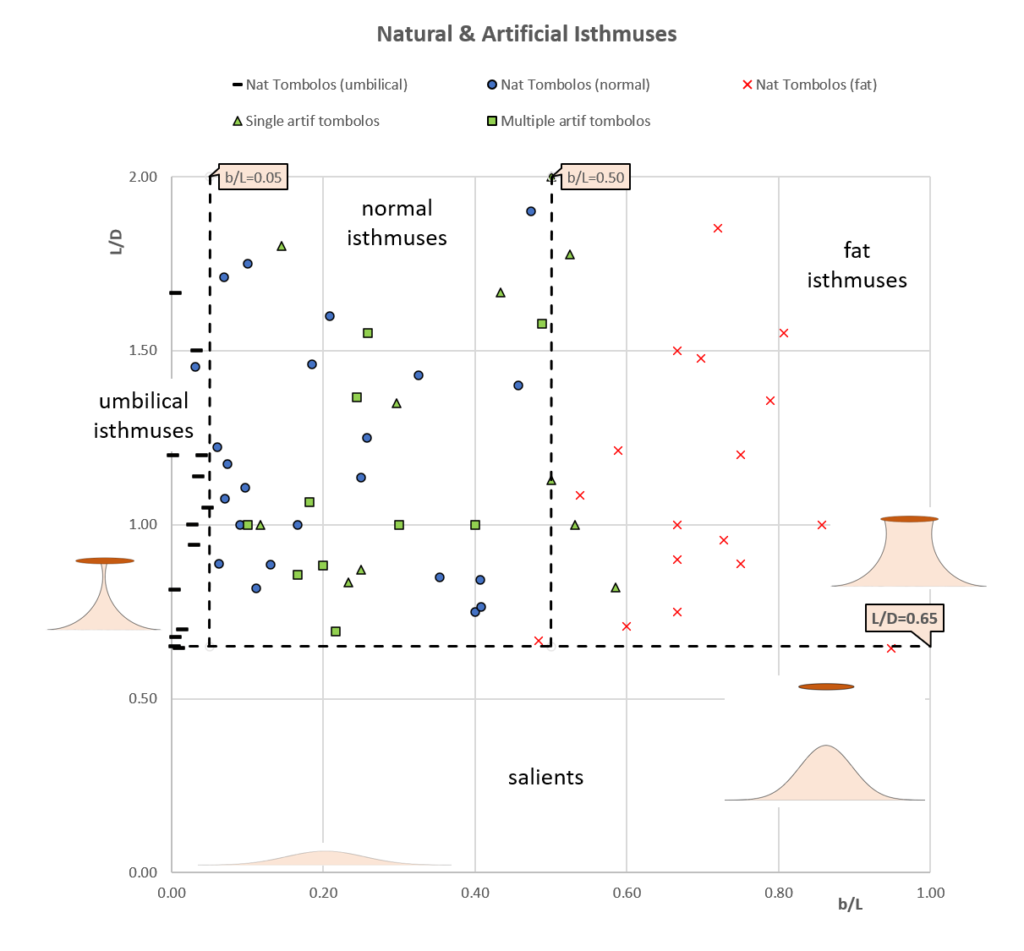
including both natural and artificial man-made structures (for L/D < 2)
Again, much scatter is found.
We can distinguish “fat” isthmuses with b/L = 0.5 to 1, and “umbilical” isthmuses with b/L < 0.05. Between these extremes, a wide area is covered by “normal” isthmuses, where artificial isthmuses nicely mix-up with natural ones, without any visible difference between single and multiple detached breakwaters.
The demarcation line between isthmuses and salients is L/D = 0.65. This result is in full agreement with several other researchers (Mangor, 2020 and Sunamura, 1987) and in line with other researchers who give wider ranges (van Rijn, 2013, Bricio, 2008, Ming, 2000).
| Isthmus: | L/D > 0.65 |
| Salient: | L/D < 0.65 |
but beware !!
Isthmuses may connect and disconnect the island or detached breakwater (i.e. become a salient) depending on wave conditions., e.g. storm waves may change an isthmus into a salient, not only due to waves turning around the breakwater’s roundheads, but also due to waves overtopping the breakwater and/or wave energy passing through the porous breakwater. This is particularly true for umbilical isthmuses with small b/L < 0.05 where the demarcation line between isthmuses and salients may range between 0.65 and 1.5.
Mediterranean salients
As mentioned above, salients are found for L/D smaller than 0.65, and we may have a look at the relationship between the dimensionless parameters L/D and d/D:
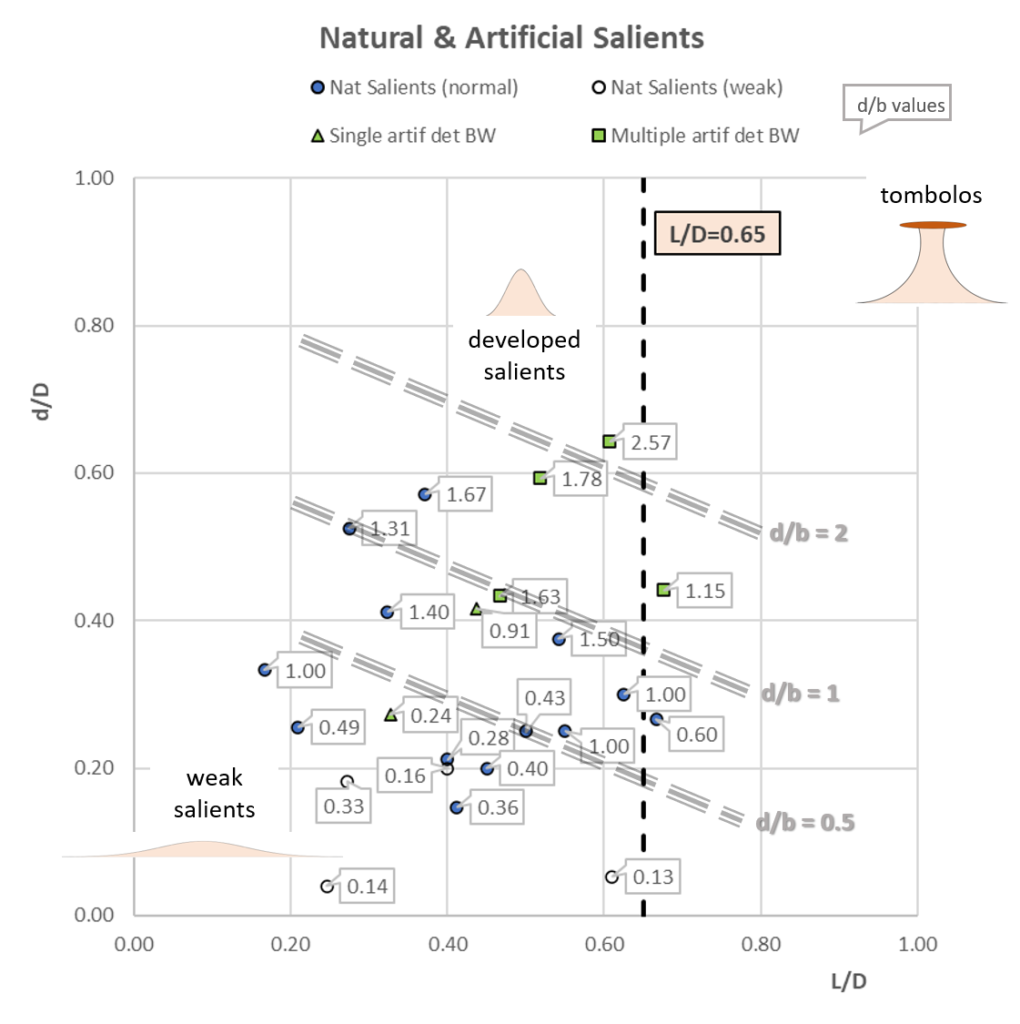
Strictly speaking, isthmuses are formed when d/D = 1 and L/D > 0.65, that is in the upper right of the figure above. We can distinguish “weak” salients with small d/D, and “developed” salients with larger d/D. The tags show the values of d/b and a trend is visible as shown by the oblique lines.
It may be observed from the figure above that salients located behind multiple artificial detached breakwaters have d/b values ranging between 1 and 2. Both salients located behind a single artificial detached breakwater have lower d/b values of 0.24 (Salou, Spain) and 0.91 (Altafulla, Spain). Natural salients have d/b values ranging between 0.14 (Mar Menor, Spain) and 1.50 (Corfu) and even 1.67 (Maaten al-Uqla, Libya).
Effects of wave climate
.
The large scatter found in the above results is a bit frustrating and we might ask if the wave climate has some effects on the shape of isthmuses and salients, e.g. one third of the umbilical isthmuses are located in areas sheltered from offshore waves … but two thirds are not!
.
The isthmus shape-changes due to periodical storms make any assessment of a Google Earth picture somewhat tricky because we do not know if it was taken just before or just after a storm. However, Google Earth usually provides at least half a dozen pictures taken at different times over the past 20 years and we are able to estimate some movements of isthmuses and salients.
Altafulla is located around 10 km NE of Tarragona (Spain) and features a beautiful salient with L/D = 0.44 and b/L = 1.05, sheltered by a 105 m detached breakwater. It seems that during the winter 2016-2017 the tip of the salient moved ca. 40 m from SW to NE, showing that the waves came mainly from SE in September 2016 and from SW in March 2017.
Although the tip of the Altafulla salient moved during a winter season, and although it is observed also that b varied from 85 m to twice this value during a period of 5 years, the overall shape did not change much and we may consider that all isthmuses and salients found on Google Earth are in a state of long-term dynamic equilibrium.
A first step to find out how the wave climate interacts with the isthmus- and salient shapes, would be to measure the “Dean number” for each site [De = H0/Vf /T, with H0: offshore wave height (m), T: wave period (s), Vf: fall velocity of sediment in water (m/s)] or possibly even better, the “Dalrymple number” [Da = gH02 /Vf3/T]. These parameters are dimensionless and include the effect of both waves and coastal sediment. As we do not have their values for each site, we used a more regional approach, comparing shapes of isthmuses and salients located in various parts of the Mediterranean area (eastern Spain, southern France, western Italy, south Aegean, Levant, North Africa) and on the Pacific Ocean between Vancouver and Cape Horn.
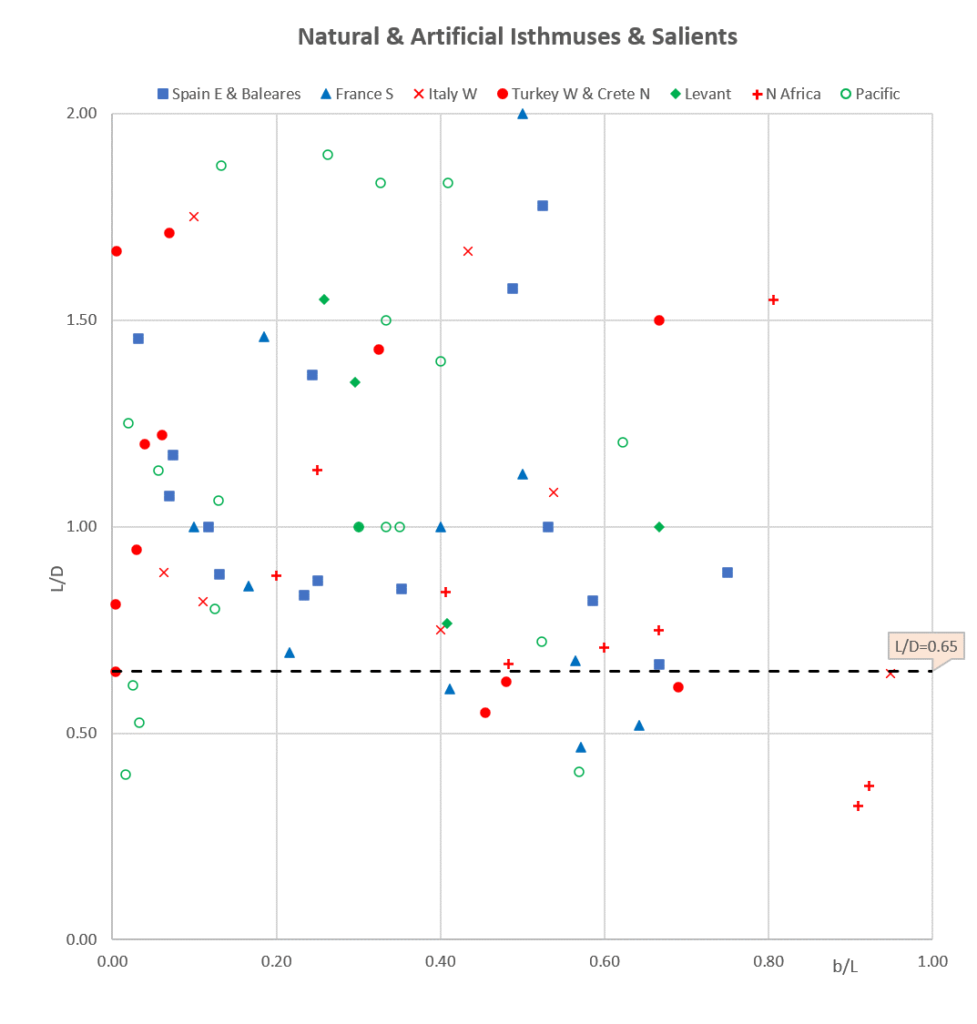
The figure above does not show any groups of isthmus-shapes (in terms of L/D versus b/L) for the selected areas, and we have to conclude that local wave climate differences seem to have no effect.
Moreover, Sunamura’s model-test results (their fig. 3 & 4) can be re-interpreted as showing no influence at all of their “K” parameter including wave effects.
In other words, the wave climate (and perhaps even the sediment grain size) does not seem to affect the final equilibrium shape of tombolos and salients. It might then be considered that waves affect only the speed of shape evolutions, and not the final equilibrium state, but this does not sound very realistic as we know that wave parameters (e.g. wave steepness) and sediment grain size both have an influence on beach slopes.
In any case, a much finer approach is probably needed, and the last word has certainly not yet been said …
One of the threads might to make a better distinction between isthmuses grown out from a salient with wave crests parallel to the initial coastline, and isthmuses made of two separated spits generated by different wave climates on each side of the final isthmus. And that might be a matter of size, e.g., islands whose length (L) is greater than several times the offshore wavelength (L0) show a very limited diffraction zone and are therefore governed by the local wave climate hitting that side of the isthmus.
References
BROCARD, G., et al., 2024, “Double tombolo formation by regressive barrier widening and landside submergence: The case of Orbetello, Italy”, Marine Geology 477 (2024) 107415, Elsevier, (20 p).
MANGOR, K., 2020, “Detached breakwaters – MarineSpecies Introduced Traits”, Wiki, http://www.marinespecies.org/introduced/wiki/Detached_breakwaters
For single detached breakwaters:
Isthmus: L/D > 0.9 to 1.0
Salient: L/D < 0.6 to 0.7
VAN RIJN, L., 2013, “Design of hard coastal structures against erosion”, www.leovanrijn-sediment.com
For multiple detached breakwaters:
Isthmus: L/D > 2
Salient: L/D = 0.5 to 2
Weak salient: L/D = 0.2 to 0.5
no effect: L/D < 0.2
BRICIO et al., 2008, “Geometric Detached Breakwater Indicators on the Spanish Northeast Coastline”, Journal of Coastal Research, Vol. 24, N° 5, (p 1289-1303).
For 27 multiple detached breakwaters on the Catalan coast:
Isthmus: L/D > 1.3
Salient: L/D = 0.5 to 1.3
Limited response: L/D < 0.5
MING , D., & CHIEW, Y., 2000, “Shoreline Changes behind Detached Breakwater”, Journal of Waterway, Port, Coastal, and Ocean Engineering, ASCE, (p 63-70).
From scale model tests, with interesting result on salient area.
Isthmus: L/D > 1.25
DALRYMPLE, R., 1992, “Prediction of storm/normal beach profiles”, Journal of Waterway, Port, Coastal, and Ocean Engineering, ASCE, 118 (2), (p 193-200).
“Dalrymple Nb”: gHo2/Vf3/T (Ho, T of waves, Vf is fall velocity of sediment).
MORY, M. & HAMM, L., 1997, “Wave height, setup and currents around a detached breakwater submitted to regular or random wave forcing”, Coastal Engineering, Vol. 31, (p 77-96).
ROSATI, J., 1990, “Functional Design of Breakwaters for Shore Protection: Empirical Methods”, Technical Report CERC-90-15, US Army Corps of Engineers, (49 p).
Nice overview of all formulations, but no final answers.
SUNAMURA, T. & MIZUNO , O., 1987, “A study on depositional shoreline forms behind an island”, Ann. Rep., Inst. Geosci., Univ. Tsukuba, N° 13, (p 71-73).
For 23 natural islands in Japan:
Isthmus: L/D > 0.67
Salient: L/D = 0.3 to 0.67
Limited response: L/D < 0.3
SUH, K. & DALRYMPLE, R., 1987, “Offshore Breakwaters in Laboratory and Field”, Journal of Waterway, Port, Coastal, and Ocean Engineering, ASCE, (p 105-121).
Scale model tests and some field data.
ROSEN, D. & VAJDA, M., 1982, “Sedimentological Influences of Detached Breakwaters”, Coastal Engineering Conference, (p 1930-1949), (fig 8).
For single detached breakwaters:
Isthmus a/D = 0.33 L/D (a is sand-free distance along inner side of BW).
DALRYMPLE, R., 1976, “Study of equilibrium beach profiles”, Coastal Engineering Conference, (p 1277-1296).
“Dean Nb”: H0/Vf T (H0, T of waves, Vf is fall velocity of sediment).