Measuring latitudes with the sun
The ancients have of course much observed the sun, its cycles and remarkable points in the sky, mostly at noon when the sun is, by definition, at its daily highest point, called ‘zenith’.
What is of interest to us here is to find the latitude of a given location (see also the section on Ptolemy).
Let’s consider the earth’s yearly track around the sun on an ellipse. The earth also rotates on itself. The axis of the earth is inclined on the plane of its orbit around the sun with an angle of around 23° 26’ and this orientation is constant during one revolution around the sun. Consequently, during one half of the year the northern hemisphere is more inclined to the sun than the southern hemisphere, with a maximum on June 21st. During the other half of the year the southern hemisphere is more inclined to the sun than the northern hemisphere, with a maximum on December 22nd. These maxima are called solstices. On these dates, the sun at noon is at its highest above the horizon on June 21st and at its lowest on December 22nd (in the northern hemisphere).
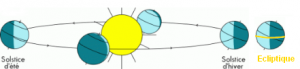
At these two solstices, the Sun at noon is, by definition, vertical above the Tropic of Cancer (around June 21st) and vertical above the Tropic of Capricorn (around December 22nd). The ancients said that “there is no shade at noon”; today we say that the sun is at its zenith. Between these two dates, the sun at noon is vertical above the equator on two days called equinoxes (around March 21st and September 23rd); we say that the declination of the sun is nil on these two dates. The sun at noon is in fact every day vertical of a point located between both tropics, and this happens twice a year for every location. E.g. the sun is vertical of a point located at 17° of latitude 45 days before and 45 days after the solstice and this fits Pliny’s description of Ptolemais Theron (Pliny the Elder, Natural History, 2, 75 & 6, 34), but this place is now better located at Agig-Adobana at 18.2° of latitude north.
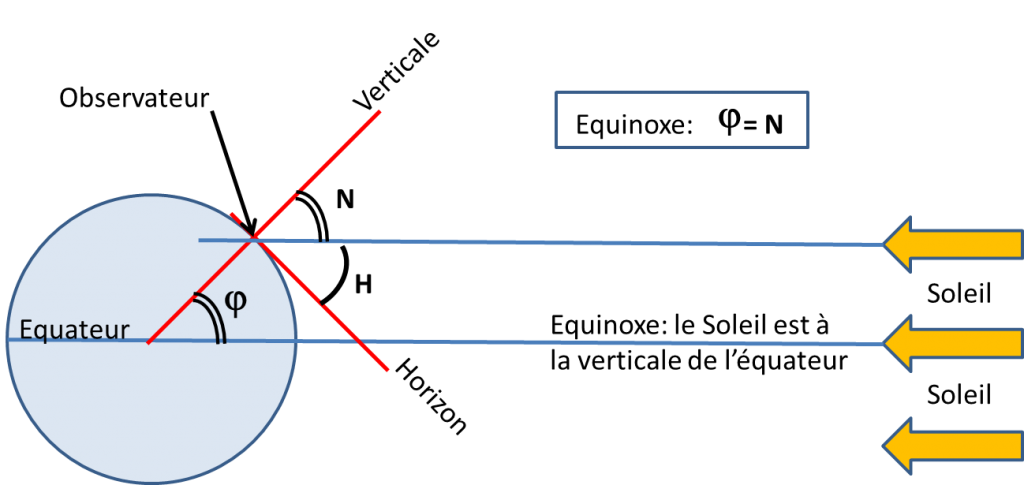
If one measures the angle H of the sun on the horizon at an equinox (when the sun at noon is above the equator), one in fact measures the complement of the latitude, thus:
Latitude phi = 90° – H measured
Measuring latitudes with Polaris
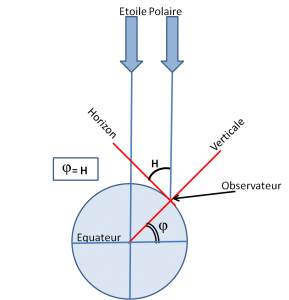
Another method is to measure the height of Polaris above the horizon. A similar exercise as measuring the latitude with the sun shows that:
Latitude phi = H measured
The precession of the equinoxes shifts the celestial system by around 50 seconds of arc per year (or 28° in 2000 years). This variation is due to a slow conical movement of the rotation axis of the earth (one full turn in 25 800 years). This means that the earth’s axis does not always point to the same location in the sky. In other words, todays ‘north star’ has not always been on the earth’s axis.
In fact, today’s north star, Polaris, is at less than 1° of the earth’s axis, but ancient astronomers had no bright north star available.
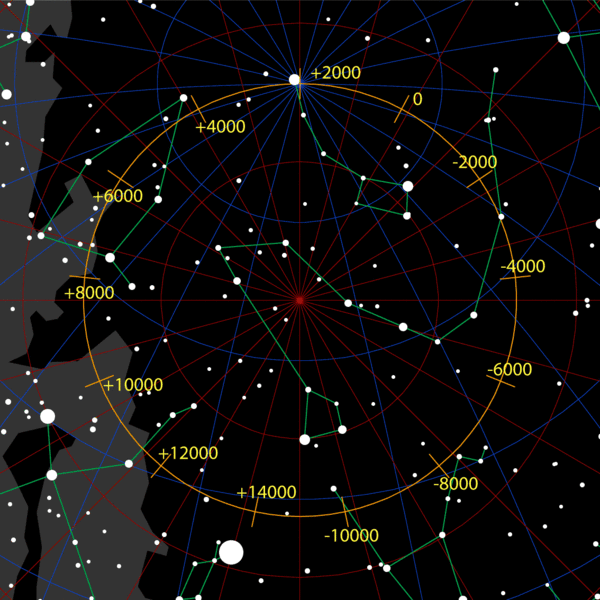
Ancient seafarers looked for “Cynosura” (Lesser Bear or Ursa Minor) to find the north at night (see Lucan, La Pharsale, Book 8) and looked for the sun at zenith for the south in daytime. Cynosura, being close to the earth’s axis, moves little during the night and is therefore quite convenient as a landmark in the night sky.
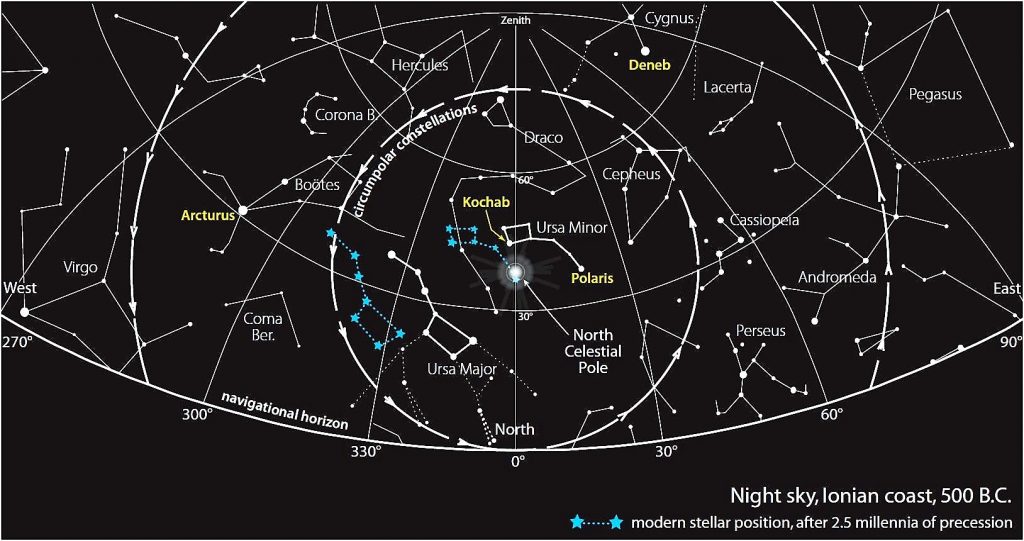
Obviously, this is not very accurate navigation: if you are sailing at 45° latitude (e.g. somewhere between the Danube estuary and Crimea) and heading north, Cynosura will be at 45° above the horizon. Seen from the position of the helmsman on board, near the stern, he will see Cynosura behind the mast of his ship, around halfway the mast height. When moving further north, increasing his latitude, Cynosura will appear higher above the horizon and higher behind the mast. If he is sailing eastbound, he will keep Cynosura to his left, on the ‘port side’ of his ship, like Odysseus after leaving Calypso’s island:
“he sat and guided his raft skilfully with the steering-oar, nor did sleep fall upon his eyelids, as he watched the Pleiads, and late-setting Bootes, and the Bear, which men also call the Wain, which ever circles where it is and watches Orion, and alone has no part in the baths of Ocean. For this star Calypso, the beautiful goddess, had bidden him to keep on the left hand as he sailed over the sea.” (Homer, Odyssey, 5, 270).
Further reading:
Information accessible to non-specialists in astronomy is available in textbooks on sundials (e.g. by Denis Savoie, 2003, ed. Belin, France) and, of course, on Wikipedia.
See also Journès & Georgelin, 2000, “Pythéas, explorateur et astronome”, ed. Nerthes, Ollioules, France, for fascinating explanations on Pytheas’ astronomy.
Danny Lee Davis, 2009, “Commercial Navigation in the Greek and Roman World”, PhD thesis, University of Texas, Austin, (359 p).